Cari studenti e care studentesse, ora che avete aperto la lettera posso svelare il piccolo sotterfugio; avevo voglia di parlarvi di fisica, ma se avessi usato come titolo “Una proprietà interessante del moto di un corpo soggetto ad una forza radiale proporzionale all’inverso del quadrato della distanza” in pochi avreste avuto voglia di leggere. Perdonate l’inganno di un prof che sente la vostra mancanza.
Come sapete le orbite chiuse seguite da un pianeta intorno al sole sono ellissi (prima legge di Keplero), come in figura
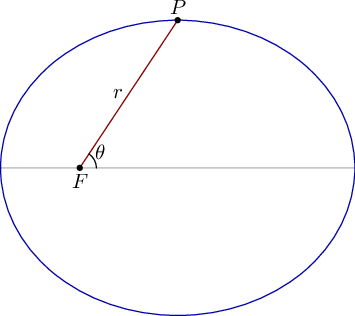
dove il sole occupa il fuoco $F$.
Scrivendo la seconda legge della dinamica ed usando la forza di attrazione gravitazionale newtoniana otteniamo
$$ m \dot{\mathbf{v}} = - \frac{GMm}{r^2} \mathbf{\hat{r}} $$
dove, vi ricordo, il punto indica la derivata rispetto al tempo, $m$ è la massa del pianeta (che si semplifica), $M$ la massa del sole ed il simbolo $\mathbf{\hat{r}}$ indica il versore radiale, ovvero il vettore di lunghezza unitaria che parte dal centro verso il punto considerato (il segno meno è dovuto alla natura attrattiva della gravità). Usando le componenti $x$ ed $y$ possiamo scrivere
$$ \dot{v}_x = - \frac{GM}{r^2} \cos{\theta} $$
$$ \dot{v}_y = - \frac{GM}{r^2} \sin{\theta} $$
A questo punto moltiplichiamo al secondo membro sia il numeratore che il denominatore per $\dot{\theta}$ ottenendo
$$ \dot{v}_x = - \frac{GM}{r^2\dot{\theta}} \dot{\theta}\cos{\theta} $$
$$ \dot{v}_y = - \frac{GM}{r^2\dot{\theta}} \dot{\theta}\sin{\theta} $$
Il termine $r^2\dot{\theta}$ è costante; si tratta infatti del momento angolare rispetto a $F$ diviso la massa $m$, momento angolare che si conserva perché la forza è sempre radiale. Vedendolo da un altro punto di vista è facile dimostrare che questo termine è proporzionale alla velocità areolare del pianeta, velocità che per la nota seconda legge di Keplero è costante (esercizio per casa).
Chiamando dunque $r^2\dot{\theta} = l$ con $l$ costante e ricordando le proprietà di derivazione di seno e coseno, riscriviamo le equazioni del moto in questa forma
$$ \dot{v}_x = - \frac{GM}{l} \dot{(\sin{\theta})} $$
$$ \dot{v}_y = \frac{GM}{l} \dot{(\cos{\theta})} $$
Portiamo a sinistra e ricordando che la somma delle derivate è la derivata della somma (linearità della derivazione) otteniamo
$$ \frac{ {\rm d} }{ {\rm d} t} \left( v_x + \frac{GM}{l} \sin{\theta} \right) = 0 $$
$$ \frac{ {\rm d} }{ {\rm d} t} \left( v_y - \frac{GM}{l} \cos{\theta} \right) = 0 $$
e dunque, ricordando che una funzione a derivata nulla è uguale ad una costante, otteniamo
$$ v_x + \frac{GM}{l} \sin{\theta} = k_x $$
$$ v_y - \frac{GM}{l} \cos{\theta} = k_y $$
con $k_x$ e $k_y$ costanti. Ultimo sforzo, con semplice passaggio otteniamo
$$ v_x - k_x = - \frac{GM}{l} \sin{\theta} $$
$$ v_y - k_y = \frac{GM}{l} \cos{\theta} $$
Eleviamo al quadrato e sommiamo, otteniamo (ricordando la relazione fondamentale della goniometria)
$$ (v_x - k_x)^2 + (v_y - k_y)^2 = \left(\frac{GM}{l}\right)^2 $$
Ed ecco il risultato interessante di cui parlavo all’inizio: nello spazio delle velocità $(v_x,v_y)$ l’orbita è una circonferenza, qualunque sia la forma dell’ellisse nello spazio $(x,y)$. La circonferenza ha centro in $(k_x,k_y)$ e raggio pari a $\frac{GM}{l}$. Questo risultato (che io sappia ottenuto a fine ottocento da Hamilton per la prima volta) si applica ovviamente non solo ad un pianeta intorno al sole, ma a qualsiasi moto soggetto ad una forza gravitazionale newtoniana. La forma dell’orbita nello spazio delle velocità prende il nome di odografo; abbiamo appena dimostrato che l’odografo per le orbite newtoniane dei pianeti è una circonferenza. Vi lascio alcuni esercizi per le vacanze:
- dimostrare che, nelle condizioni qui proposte, $k_x = 0$ e $k_y$ è pari al raggio della circonferenza moltiplicato per l’eccentricità dell’orbita;
- cosa succede se l’orbita non è chiusa, ovvero è una parabola o un’iperbole? Se vi sforzate un po' scoprirete che anche in questo caso nello spazio delle velocità la traiettoria è una circonferenza (o meglio un arco di circonferenza).
Non trovate anche voi meraviglioso questo risultato? Bon voyage.
P.S.
Riguardo allo ius soli non so come la pensiate e non è importante che io lo sappia. So però che ognuno di voi si sarà formato un’idea basata sul proprio sentire e le proprie convinzioni, non per moda o ideologia altrui. Questo mi basta.