Ho rinunciato alla pace interiore per rendere la mia mente un luogo pieno di ombre.
– Luthen Rael
Caro L
non so se leggi ancora queste mie lettere, ma mi piace pensarlo. Ieri sera, mentre preparavo un compito di prova per le mie quinte (ti piacerebbero, alcuni ti somigliano) ho pensato ad un problema che sono sicuro ti sarebbe interessato da studente. Sono partito da una domanda semplice: come collegare un certo numero di resistenze da \(1\) ohm in modo da avere una resistenza totale equivalente pari a \(7/3\) ohm. Usando collegamenti in serie e in parallelo la risposta è piuttosto immediata. Poi mi è venuto in mente di chiedere se fosse possibile in modo analogo ottenere una resistenza pari a un qualsiasi numero razionale positivo. Ed ecco la risposta, semplice e (a mio avviso) elegante.
Sappiamo che collegando due resistenze in serie si ha una resistenza equivalente data dalla somma
\[ R_{tot} = R_1 + R_2 \]
Sappiamo anche che collegando due resistenza in parallelo si ha una resistenza il cui reciproco è la somma dei reciproci
\[ R_{tot} = \frac{R_1 R_2}{R_1+R_2} \]
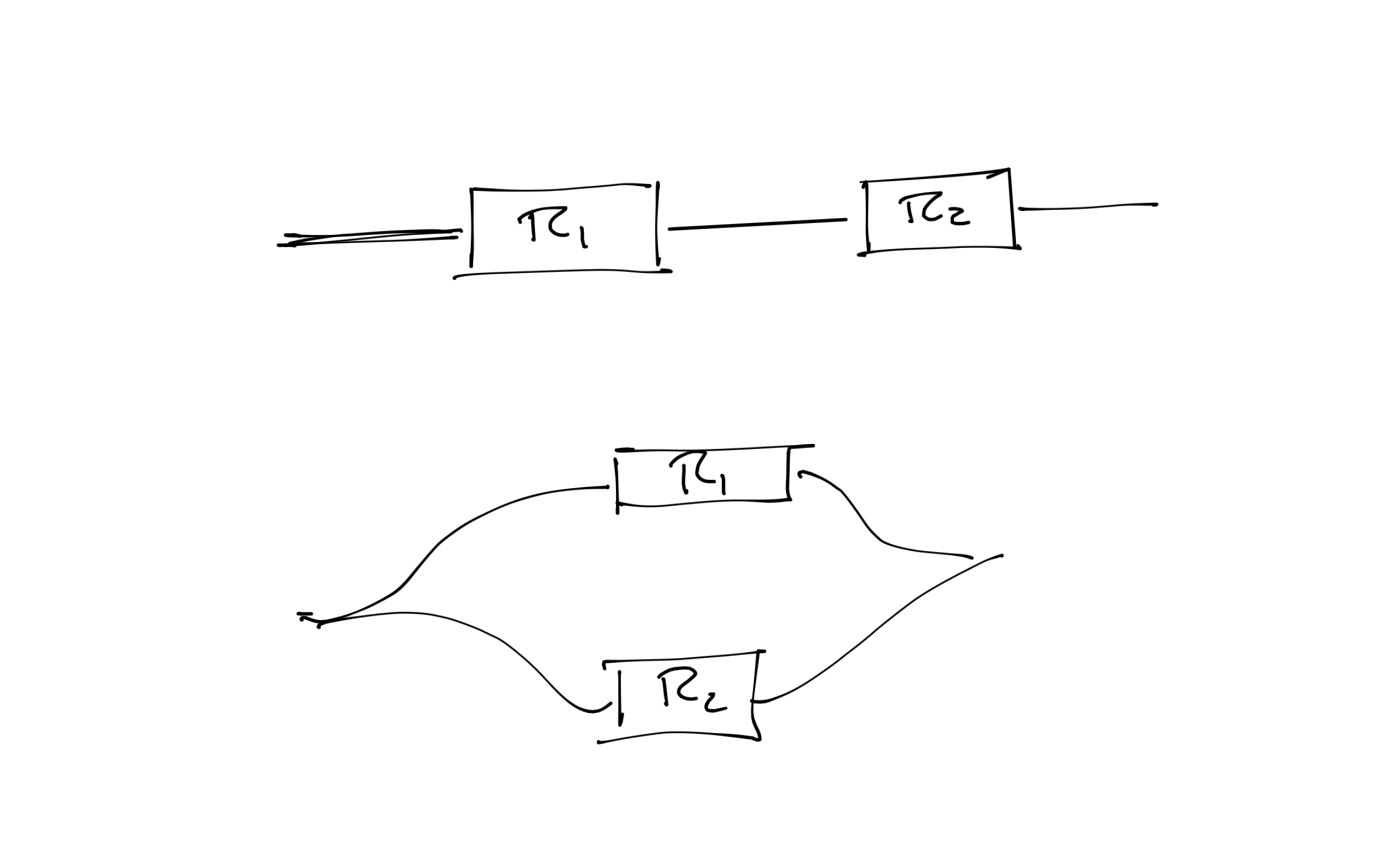
Immaginiamo dunque di avere una resistenza con valore razionale \(R=\frac{p}{q}\); se la mettiamo in serie con una resistenza da \(1\) ohm otterremo
\[ R_{tot} = \frac{p}{q} + 1 = \frac{p+q}{q}; \]
se la mettiamo in parallelo con una resistenza da \(1\) ohm otterremo
\[ R_{tot} = \frac{\frac{p}{q}}{\frac{p}{q} + 1} = \frac{p}{p+q} \]
Queste sono esattamente le due operazioni che permettono di costruire a partire dal numero \(1\) tutti i numeri razionali in quello che si chiama albero di Calkin-Wilf (di cui ho già parlato 1).
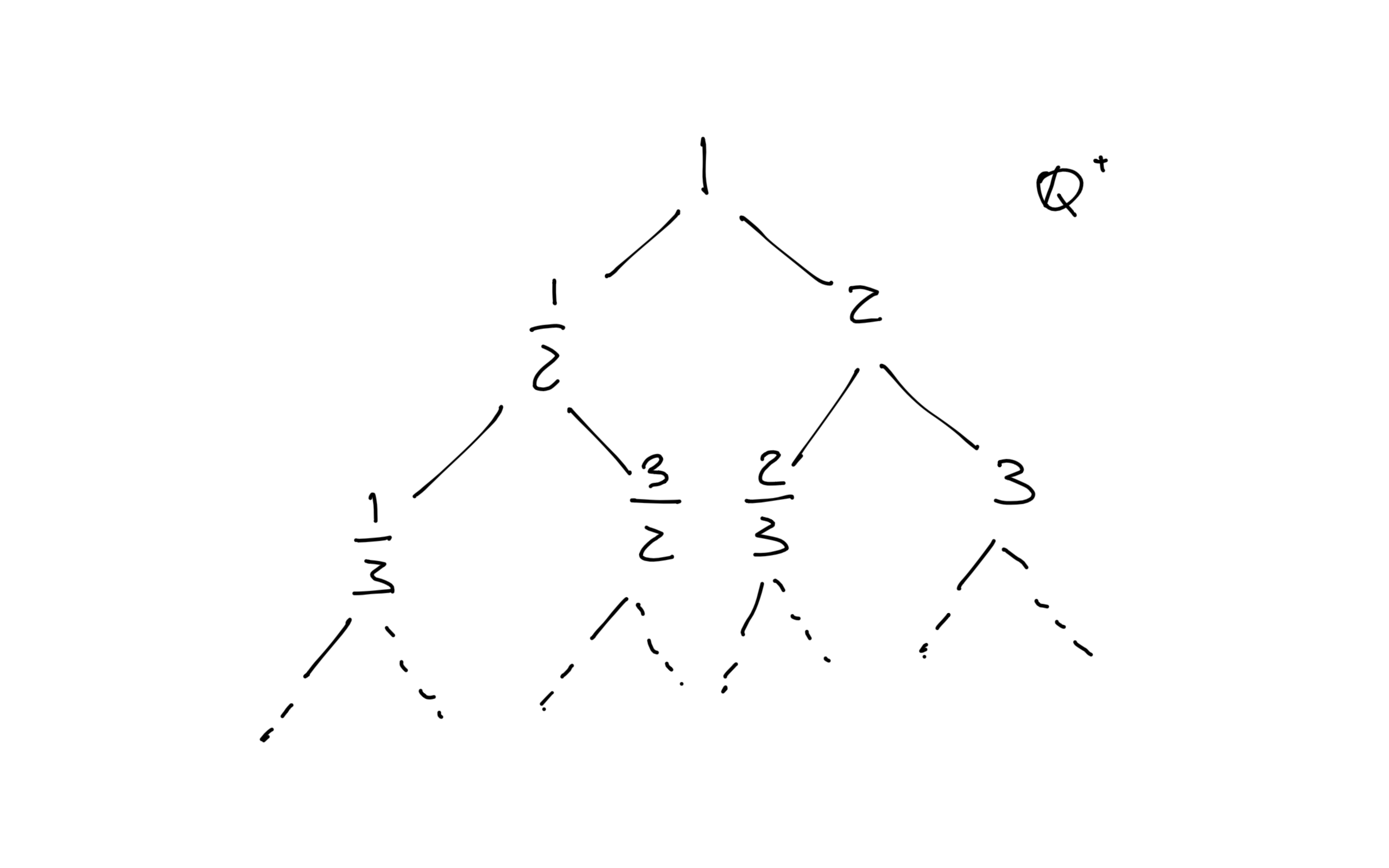
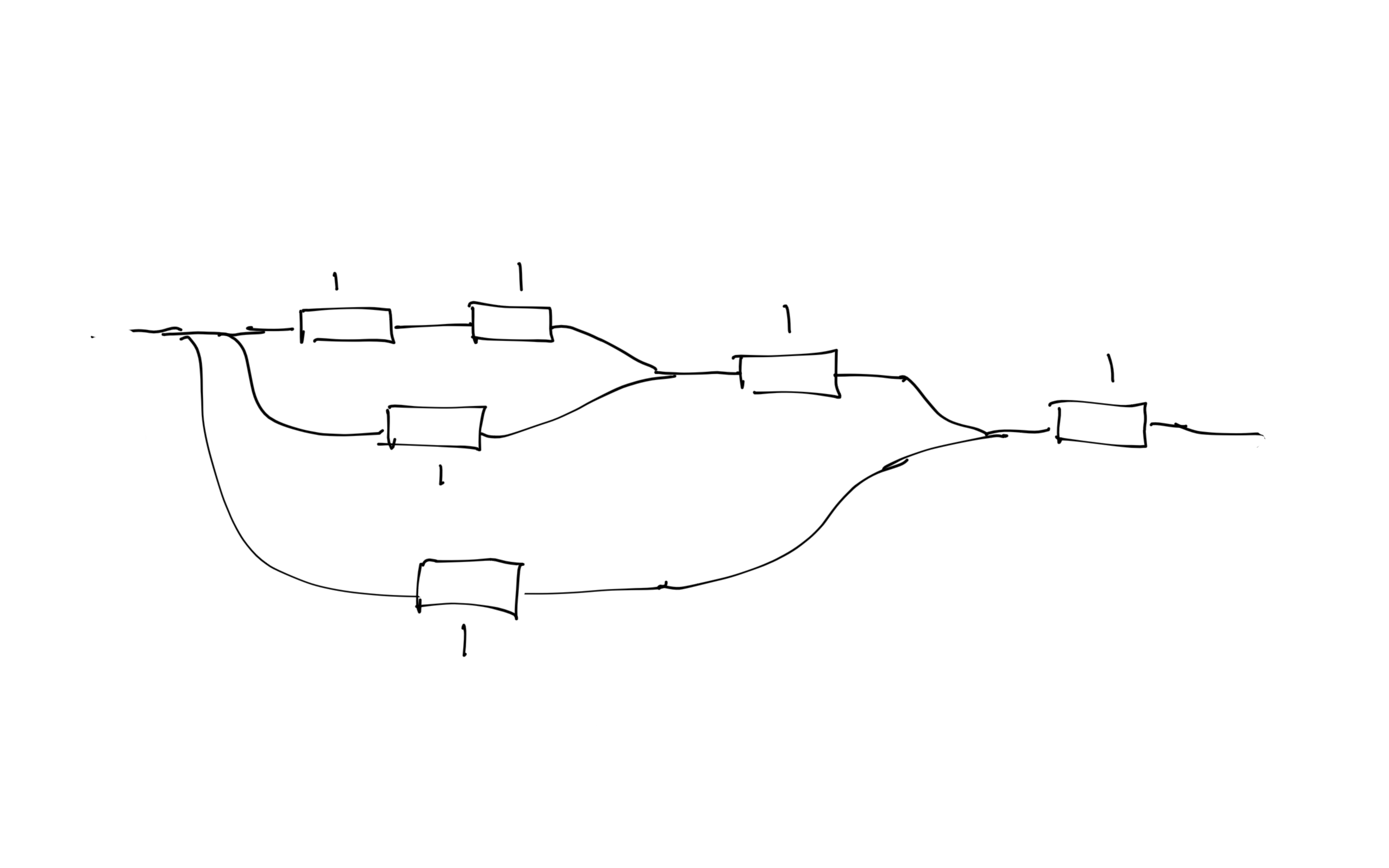
Dunque componendo in serie e in parallelo resistenze da \(1\) ohm posso ottenere un qualsiasi numero razionale. E siccome gli irrazionali sono rami infiniti sull’albero di Calkin-Wilf, componendo infinite resistenze in serie e in parallelo posso ottenere una resistenza equivalente irrazionale qualsiasi. Per esempio se parto da una resistenza da \(1\) ohm e metto in serie con un’altra da \(1\) ohm ottengo una da \(2\) ohm. Se questo sistema lo compongo in parallelo con una da \(1\) ohm ottengo una da \(2/3\) ohm. Se metto in serie ad un’altra da \(1\) ohm diventa in totale \(5/3\) ohm, un’altra in parallelo diventa \(5/8\), un’altra in serie diventa \(13/8\) etc etc. Riconoscerai i rapporti tra numeri successivi della serie di Fibonacci, rapporti che convergono al numero irrazionale aureo.
Il territorio da esplorare è ampio, ma la lettera è finita. Questo esempio banale rafforza però una mia idea di cui spesso vi parlavo in classe (e ogni tanto ancora lo faccio): i compiti in classe non sono atti burocratici o procedure selettive standardizzate, sono piccoli manifesti di intenti, luoghi di incontro e scontro, frontiere da attraversare e ridisegnare. Te li ricordi le nostre frontiere? Ti ricordi l’aula in fondo al corridoio?
Io non ricordo più molto. Non ricordo più il tuo volto, la tua voce è diventata quella di una folla che ti ha sostituito in tutti questi anni. Non penso molto a te, ma quando succede ritorna improvviso il suono del telefono che squilla la sera tardi. In quell’istante esatto mi manchi.